Draw Circle Between Points Tikz
The TigrandZ and PGF Packages
Transmission for version iii.1.9a
TikZ
\(\newcommand{\footnotename}{footnote}\) \(\def \LWRfootnote {one}\) \(\newcommand {\footnote }[2][\LWRfootnote ]{{}^{\mathrm {#one}}}\) \(\newcommand {\footnotemark }[1][\LWRfootnote ]{{}^{\mathrm {#1}}}\) \(\let \LWRorighspace \hspace \) \(\renewcommand {\hspace }{\ifstar \LWRorighspace \LWRorighspace }\) \(\newcommand {\mathnormal }[1]{{#1}}\) \(\newcommand \ensuremath [one]{#1}\) \(\newcommand {\LWRframebox }[2][]{\fbox {#two}} \newcommand {\framebox }[i][]{\LWRframebox } \) \(\newcommand {\setlength }[2]{}\) \(\newcommand {\addtolength }[2]{}\) \(\newcommand {\setcounter }[2]{}\) \(\newcommand {\addtocounter }[2]{}\) \(\newcommand {\standard arabic }[1]{}\) \(\newcommand {\number }[1]{}\) \(\newcommand {\noalign }[ane]{\text {#1}\notag \\}\) \(\newcommand {\cline }[1]{}\) \(\newcommand {\directlua }[1]{\text {(directlua)}}\) \(\newcommand {\luatexdirectlua }[1]{\text {(directlua)}}\) \(\newcommand {\protect }{}\) \(\def \LWRabsorbnumber #1 {}\) \(\def \LWRabsorbquotenumber "#ane {}\) \(\newcommand {\LWRabsorboption }[i][]{}\) \(\newcommand {\LWRabsorbtwooptions }[1][]{\LWRabsorboption }\) \(\def \mathchar {\ifnextchar "\LWRabsorbquotenumber \LWRabsorbnumber }\) \(\def \mathcode #i={\mathchar }\) \(\let \delcode \mathcode \) \(\permit \delimiter \mathchar \) \(\def \oe {\unicode {x0153}}\) \(\def \OE {\unicode {x0152}}\) \(\def \ae {\unicode {x00E6}}\) \(\def \AE {\unicode {x00C6}}\) \(\def \aa {\unicode {x00E5}}\) \(\def \AA {\unicode {x00C5}}\) \(\def \o {\unicode {x00F8}}\) \(\def \O {\unicode {x00D8}}\) \(\def \50 {\unicode {x0142}}\) \(\def \50 {\unicode {x0141}}\) \(\def \ss {\unicode {x00DF}}\) \(\def \SS {\unicode {x1E9E}}\) \(\def \dag {\unicode {x2020}}\) \(\def \ddag {\unicode {x2021}}\) \(\def \P {\unicode {x00B6}}\) \(\def \copyright {\unicode {x00A9}}\) \(\def \pounds {\unicode {x00A3}}\) \(\permit \LWRref \ref \) \(\renewcommand {\ref }{\ifstar \LWRref \LWRref }\) \( \newcommand {\multicolumn }[three]{#3}\) \(\require {textcomp}\) \( \newcommand {\meta }[i]{\langle \textit {#1}\rangle } \) \(\newcommand {\intertext }[1]{\text {#1}\notag \\}\) \(\allow \Hat \hat \) \(\let \Check \cheque \) \(\let \Tilde \tilde \) \(\let \Acute \acute \) \(\let \Grave \grave \) \(\let \Dot \dot \) \(\let \Ddot \ddot \) \(\let \Breve \breve \) \(\let \Bar \bar \) \(\let \Vec \vec \)
thirteenSpecifying Coordinates
13.1Overview¶
A coordinate is a position on the canvas on which your motion-picture show is drawn. TikZ uses a special syntax for specifying coordinates. Coordinates are always put in circular brackets. The full general syntax is ( [ ⟨ options ⟩ ] ⟨ coordinate specification ⟩ ) .
The ⟨ coordinate specification ⟩ specifies coordinates using one of many different possible coordinate systems. Examples are the Cartesian coordinate system or polar coordinates or spherical coordinates. No matter which coordinate system is used, in the finish, a specific point on the sail is represented by the coordinate.
There are two means of specifying which coordinate system should exist used:
- Explicitly
-
You tin can specify the coordinate organization explicitly. To do and so, you requite the name of the coordinate system at the starting time, followed by cs:, which stands for "coordinate system", followed by a specification of the coordinate using the fundamental–value syntax. Thus, the general syntax for ⟨ coordinate specification ⟩ in the explicit instance is ( ⟨ coordinate organization ⟩ cs: ⟨ list of key–value pairs specific to the coordinate organisation ⟩ ).
- Implicitly
-
The explicit specification is often too verbose when numerous coordinates should be given. Because of this, for the coordinate systems that you lot are probable to use often a special syntax is provided. Ti1000Z volition detect when yous utilise a coordinate specified in a special syntax and volition choose the correct coordinate arrangement automatically.
Here is an example in which explicit the coordinate systems are specified explicitly:
In the adjacent example, the coordinate systems are implicit:
Information technology is possible to requite options that apply only to a single coordinate, although this makes sense for transformation options only. To give transformation options for a single coordinate, give these options at the outset in brackets:
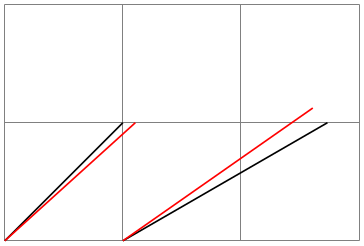
13.2Coordinate Systems¶
13.2.1Canvas, XYZ, and Polar Coordinate Systems¶
Let united states outset with the basic coordinate systems.
Coordinate organization canvas ¶
The simplest way of specifying a coordinate is to utilize the canvas coordinate arrangement. Y'all provide a dimension \(d_x\) using the 10= option and another dimension \(d_y\) using the y= choice. The position on the sheet is located at the position that is \(d_x\) to the correct and \(d_y\) above the origin.
/tikz/cs/x = ⟨ dimension ⟩ (no default, initially 0pt) ¶
Altitude by which the coordinate is to the right of the origin. Yous can also write things similar 1cm+2pt since the mathematical engine is used to evaluate the ⟨ dimension ⟩.
/tikz/cs/y = ⟨ dimension ⟩ (no default, initially 0pt) ¶
Distance by which the coordinate is above the origin.
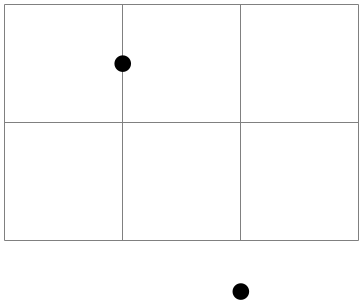
To specify a coordinate in the coordinate system implicitly, y'all use two dimensions that are separated by a comma as in (0cm,3pt) or (2cm,\textheight).

Coordinate system xyz ¶
The xyz coordinate system allows you to specify a signal every bit a multiple of three vectors called the \(x\)-, \(y\)-, and \(z\)-vectors. By default, the \(ten\)-vector points 1cm to the right, the \(y\)-vector points 1cm upwards, but this tin be inverse arbitrarily as explained in Department 25.2. The default \(z\)-vector points to \(\bigl (-3.85\textrm {mm},-iii.85\textrm {mm}\bigr )\).
To specify the factors past which the vectors should exist multiplied before existence added, yous apply the following iii options:
/tikz/cs/x = ⟨ factor ⟩ (no default, initially 0)
Gene by which the \(x\)-vector is multiplied.
/tikz/cs/y = ⟨ factor ⟩ (no default, initially 0)
Works like ten.
/tikz/cs/z = ⟨ factor ⟩ (no default, initially 0) ¶
Works similar 10.
This coordinate system can likewise be selected implicitly. To do and then, you only provide two or three comma-separated factors (non dimensions).
Notation: It is possible to use coordinates similar (1,2cm), which are neither canvas coordinates nor xyz coordinates. The rule is the following: If a coordinate is of the implicit form ( ⟨ x ⟩ , ⟨ y ⟩ ), so ⟨ 10 ⟩ and ⟨ y ⟩ are checked, independently, whether they have a dimension or whether they are dimensionless. If both have a dimension, the canvas coordinate system is used. If both lack a dimension, the xyz coordinate arrangement is used. If ⟨ x ⟩ has a dimension and ⟨ y ⟩ has not, so the sum of two coordinate ( ⟨ x ⟩ ,0pt) and (0, ⟨ y ⟩ ) is used. If ⟨ y ⟩ has a dimension and ⟨ x ⟩ has not, then the sum of two coordinate ( ⟨ x ⟩ ,0) and (0pt, ⟨ y ⟩ ) is used.
Note furthermore: An expression like (2+3cm,0) does not mean the aforementioned as (2cm+3cm,0). Instead, if ⟨ x ⟩ or ⟨ y ⟩ internally uses a mixture of dimensions and dimensionless values, then all dimensionless values are "upgraded" to dimensions by interpreting them as pt. So, 2+3cm is the same dimension as 2pt+3cm.
Coordinate system canvas polar ¶
The canvas polar coordinate system allows you to specify polar coordinates. You provide an angle using the bending= option and a radius using the radius= option. This yields the point on the canvas that is at the given radius distance from the origin at the given degree. An angle of zippo degrees to the right, a caste of ninety upward.
/tikz/cs/angle = ⟨ degrees ⟩ (no default) ¶
The angle of the coordinate. The angle must e'er be given in degrees.
/tikz/cs/radius = ⟨ dimension ⟩ (no default) ¶
The distance from the origin.
/tikz/cs/x radius = ⟨ dimension ⟩ (no default) ¶
A polar coordinate is, later all, just a point on a circle of the given ⟨ radius ⟩. When you provide an \(ten\)-radius and likewise a \(y\)-radius, you lot specify an ellipse instead of a circle. The radius choice has the aforementioned upshot as specifying identical x radius and y radius options.
/tikz/cs/y radius = ⟨ dimension ⟩ (no default) ¶
Works like ten radius.

\tikz\draw(0,0)-- (canvas polar cs:angle=xxx,radius=1cm);
The implicit course for canvas polar coordinates is the following: you specify the bending and the distance, separated by a colon as in (30:1cm).

\tikz\draw(0cm,0cm)-- (xxx:1cm)-- (threescore:1cm)-- (xc:1cm)
-- (120:1cm)-- (150:1cm)-- (180:1cm);
Two different radii are specified by writing (xxx:1cm and 2cm).
For the implicit class, instead of an bending given every bit a number you can likewise employ certain words. For example, up is the aforementioned equally 90, so that you can write \tikz \depict (0,0) -- (2ex,0pt) -- +(up:1ex); and get  . Autonomously from up you can use down, left, right, n, south, west, east, north e, due north west, south due east, south west, all of which have their natural significant.
. Autonomously from up you can use down, left, right, n, south, west, east, north e, due north west, south due east, south west, all of which have their natural significant.
Coordinate organization xyz polar ¶
This coordinate organisation piece of work similarly to the canvas polar system. Nevertheless, the radius and the angle are interpreted in the \(xy\)-coordinate system, not in the canvas system. More detailed, consider the circle or ellipse whose half axes are given by the current \(x\)-vector and the electric current \(y\)-vector. Then, consider the point that lies at a given angle on this ellipse, where an angle of zero is the same as the \(x\)-vector and an angle of 90 is the \(y\)-vector. Finally, multiply the resulting vector by the given radius cistron. Voilà.
/tikz/cs/angle = ⟨ degrees ⟩ (no default)
The angle of the coordinate interpreted in the ellipse whose axes are the \(10\)-vector and the \(y\)-vector.
/tikz/cs/radius = ⟨ factor ⟩ (no default)
A factor by which the \(x\)-vector and \(y\)-vector are multiplied prior to forming the ellipse.
/tikz/cs/x radius = ⟨ dimension ⟩ (no default)
A specific cistron by which only the \(ten\)-vector is multiplied.
/tikz/cs/y radius = ⟨ dimension ⟩ (no default)
Works similar x radius.

\depict(0,0)-- (xyz polar cs:angle=0,radius=i); \depict(xyz polar cs:bending=0,radius=2)
\begin{tikzpicture}[x=1.5cm,y=1cm]
\draw[help lines](0cm,0cm)grid (3cm,2cm);
\depict(0,0)-- (xyz polar cs:angle=30,radius=1);
\draw(0,0)-- (xyz polar cs:angle=lx,radius=i);
\draw(0,0)-- (xyz polar cs:angle=90,radius=ane);
-- (xyz polar cs:angle=thirty,radius=ii)
-- (xyz polar cs:bending=60,radius=2)
-- (xyz polar cs:bending=ninety,radius=2);
\terminate{tikzpicture}
The implicit version of this option is the same equally the implicit version of sheet polar, only y'all do non provide a unit.

\tikz[ten={(0cm,1cm)},y={(-1cm,0cm)}]
\draw(0,0)-- (30:1)-- (threescore:1)-- (xc:1)
-- (120:1)-- (150:1)-- (180:i);
Coordinate organisation xy polar ¶
This is but an allonym for xyz polar, which some people might prefer as there is no z-coordinate involved in the xyz polar coordinates.
13.ii.2Barycentric Systems¶
In the barycentric coordinate system a indicate is expressed every bit the linear combination of multiple vectors. The thought is that you specify vectors \(v_1\), \(v_2\), …, \(v_n\) and numbers \(\blastoff _1\), \(\alpha _2\), …, \(\alpha _n\). Then the barycentric coordinate specified by these vectors and numbers is
\(\seteqnumber{0}{}{0}\)\brainstorm{align*} \frac {\blastoff _1 v_1 + \alpha _2 v_2 + \cdots + \alpha _n v_n}{\alpha _1 + \alpha _2 + \cdots + \alpha _n} \stop{align*}
The barycentric cs allows you to specify such coordinates easily.
Coordinate system barycentric ¶
For this coordinate arrangement, the ⟨ coordinate specification ⟩ should exist a comma-separated list of expressions of the course ⟨ node name ⟩ = ⟨ number ⟩. Note that (currently) the list should non comprise any spaces before or after the ⟨ node name ⟩ (different normal central–value pairs).
The specified coordinate is now computed as follows: Each pair provides one vector and a number. The vector is the centre anchor of the ⟨ node name ⟩. The number is the ⟨ number ⟩. Notation that (currently) you cannot specify a different anchor, and then that in guild to use, say, the north anchor of a node y'all offset accept to create a new coordinate at this northward anchor. (Using for instance \coordinate(mynorth) at (mynode.due north);.)
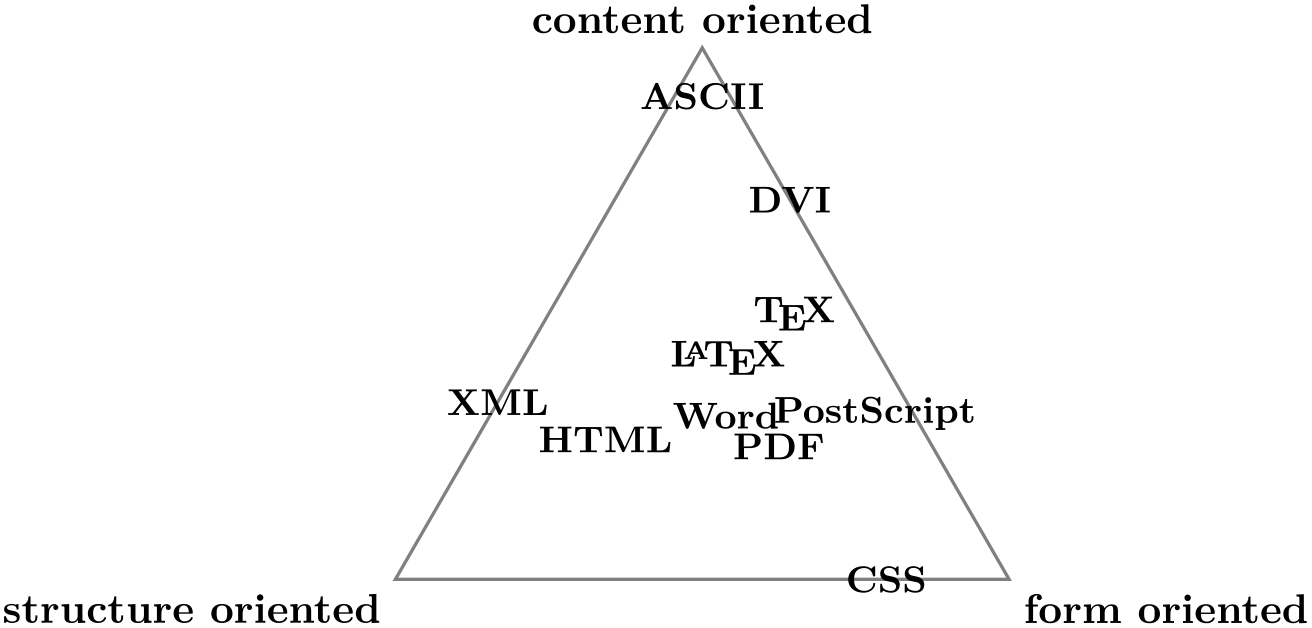
\node [above]at (content) {content oriented}; \draw [thick,gray](content.s)-- (structure.due north east)-- (class.north due west)-- cycle; \small
\begin{tikzpicture}
\coordinate(content)at (90:3cm);
\coordinate(structure)at (210:3cm);
\coordinate(form)at (-30:3cm);
\node [beneath left]at (structure) {structure oriented};
\node [below correct]at (form) {course oriented};
\nodeat (barycentric cs:content=0.v,structure=0.1 ,form=1) {PostScript};
\nodeat (barycentric cs:content=1 ,structure=0 ,form=0.4) {DVI};
\nodeat (barycentric cs:content=0.v,structure=0.5 ,form=1) {PDF};
\nodeat (barycentric cs:content=0 ,construction=0.25,form=1) {CSS};
\nodeat (barycentric cs:content=0.5,structure=1 ,form=0) {XML};
\nodeat (barycentric cs:content=0.5,structure=1 ,form=0.4) {HTML};
\nodeat (barycentric cs:content=1 ,structure=0.2 ,class=0.8) {\TeX};
\nodeat (barycentric cs:content=1 ,structure=0.6 ,grade=0.viii) {\LaTeX};
\nodeat (barycentric cs:content=0.eight,structure=0.8 ,form=1) {Word};
\nodeat (barycentric cs:content=1 ,structure=0.05,course=0.05) {ASCII};
\finish{tikzpicture}
xiii.two.3Node Coordinate System¶
In pgf and in TithousandZ it is quite easy to define a node that yous wish to reference at a subsequently point. In one case you lot accept defined a node, in that location are different ways of referencing points of the node. To do and so, you use the post-obit coordinate system:
Coordinate system node ¶
This coordinate system is used to reference a specific betoken inside or on the border of a previously defined node. It can exist used in different ways, so let us go over them one by ane.
You tin can use three options to specify which coordinate y'all mean:
/tikz/cs/name = ⟨ node proper name ⟩ (no default) ¶
Specifies the node that you wish to apply to specify a coordinate. The ⟨ node name ⟩ is the proper noun that was previously used to name the node using the name= ⟨ node proper noun ⟩ choice or the special node proper noun syntax.
/tikz/anchor = ⟨ anchor ⟩ (no default) ¶
Specifies an anchor of the node. Here is an example:
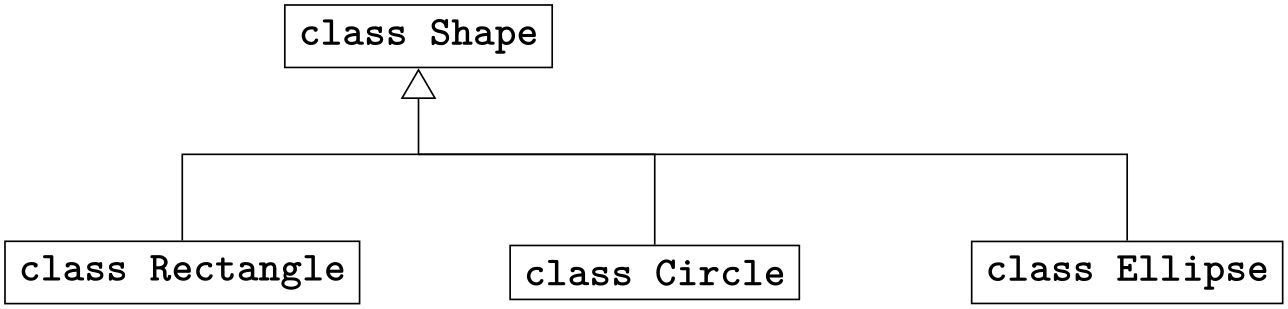
\draw(node cs:name=circle,anchor=due north)|- (0,i); \usetikzlibrary {arrows.meta}
\brainstorm{tikzpicture}
\node(shape)at (0,2) [draw] {\texttt{grade Shape}};
\node(rect)at (-2,0) [draw] {\texttt{grade Rectangle}};
\node(circle)at (2,0) [describe] {\texttt{class Circle}};
\node(ellipse)at (half dozen,0) [draw] {\texttt{course Ellipse}};
\depict(node cs:name=ellipse,ballast=north)|- (0,i);
\describe [arrows = -{Triangle[open,bending=60:3mm]}]
(node cs:name=rect,anchor=north)
|- (0,1)-| (node cs:name=shape,anchor=south);
\end{tikzpicture}
/tikz/cs/bending = ⟨ degrees ⟩ (no default)
It is besides possible to provide an angle instead of an anchor. This coordinate refers to a point of the node's edge where a ray shot from the center in the given angle hits the border. Here is an example:

It is possible to provide neither the anchor= option nor the angle= selection. In this case, TikZ will calculate an appropriate border position for y'all. Here is an example:

TikZ will be reasonably clever at determining the border points that you "hateful", but, naturally, this may fail in some situations. If TigrandZ fails to determine an appropriate border signal, the eye volition be used instead.
Automatic computation of anchors works only with the line-to operations --, the vertical/horizontal versions |- and -|, and with the curve-to operation ... For other path commands, such every bit parabola or plot, the heart volition be used. If this is not desired, you should give a named anchor or an angle anchor.
Annotation that if y'all utilize an automatic coordinate for both the showtime and the end of a line-to, as in --(node cs:proper noun=b)--, then two border coordinates are computed with a move-to between them. This is commonly exactly what y'all want.
If you lot use relative coordinates together with automatic anchor coordinates, the relative coordinates are computed relative to the node's center, non relative to the border indicate. Here is an example:

Similarly, in the following examples both command points are \((one,1)\):
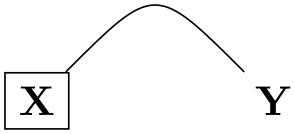
\tikz\draw(0,0)node (x) [describe] {10}
(2,0)node (y) {Y}
(node cs:name=x) ..controls + (ane,one)and + (-1,i) ..
(node cs:name=y);
The implicit way of specifying the node coordinate organization is to simply use the proper noun of the node in parentheses as in (a) or to specify a name together with an anchor or an angle separated by a dot as in (a.northward) or (a.10).
Here is a more complete example:
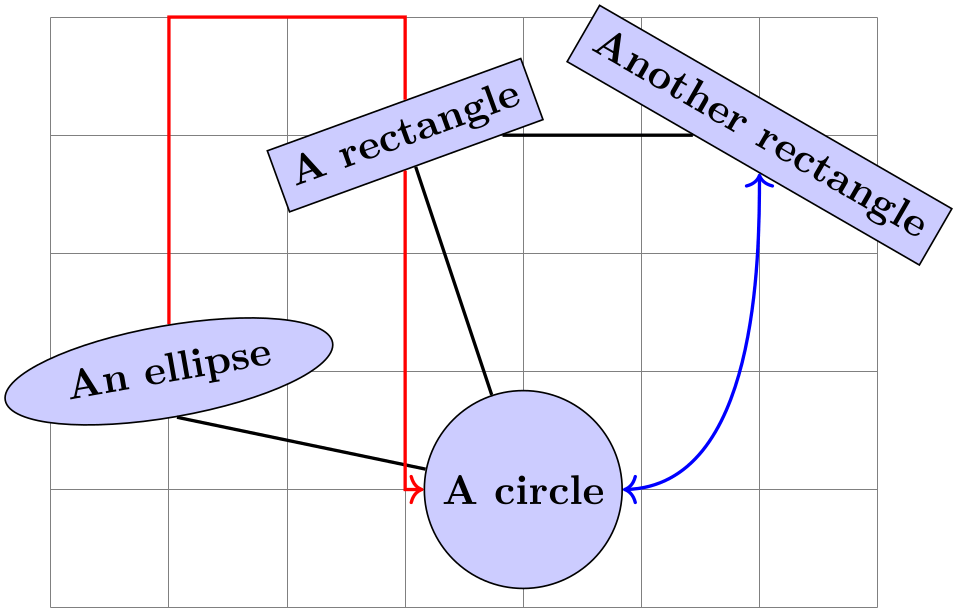
\usetikzlibrary {shapes.geometric}
\begin{tikzpicture}[fill=bluish!20]
\draw[help lines](-1,-2)grid (half-dozen,3);
\path(0,0)node (a) [ellipse,rotate=x,draw,fill] {An ellipse}
(3,-1)node (b) [circle,draw,fill up] {A circumvolve}
(ii,ii)node (c) [rectangle,rotate=20,draw,fill] {A rectangle}
(5,2)node (d) [rectangle,rotate=-30,describe,fill] {Some other rectangle};
\draw[thick](a.south)-- (b)-- (c)-- (d);
\draw[thick,cerise,->](a)|- + (i,iii)-| (c)|- (b);
\draw[thick,bluish,<->](b) ..controls + (correct:2cm)and + (down:1cm) ..(d);
\stop{tikzpicture}
13.2.4Tangent Coordinate Systems¶
Coordinate system tangent ¶
This coordinate organisation, which is available merely when the TikZ library calc is loaded, allows y'all to compute the betoken that lies tangent to a shape. In detail, consider a ⟨ node ⟩ and a ⟨ point ⟩. Now, draw a straight line from the ⟨ point ⟩ so that information technology "touches" the ⟨ node ⟩ (more than formally, so that it is tangent to this ⟨ node ⟩). The point where the line touches the shape is the indicate referred to past the tangent coordinate arrangement.
The post-obit options may be given:
/tikz/cs/node = ⟨ node ⟩ (no default) ¶
This cardinal specifies the node on whose border the tangent should lie.
/tikz/cs/signal = ⟨ indicate ⟩ (no default) ¶
This key specifies the bespeak through which the tangent should become.
/tikz/cs/solution = ⟨ number ⟩ (no default) ¶
Specifies which solution should be used if there are more than i.
A special algorithm is needed in society to compute the tangent for a given shape. Currently, tangents can be computed for nodes whose shape is one of the following:
• coordinate • circle
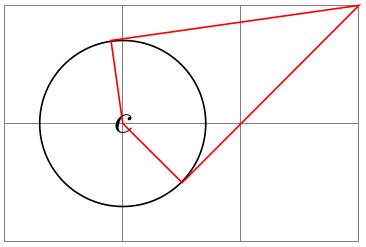
There is no implicit syntax for this coordinate organisation.
13.two.vDefining New Coordinate Systems¶
While the prepare of coordinate systems that TikZ can parse via their special syntax is fixed, it is possible and quite piece of cake to define new explicitly named coordinate systems. For this, the following commands are used:
\tikzdeclarecoordinatesystem {⟨ name ⟩}{⟨ code ⟩} ¶
This command declares a new coordinate system named ⟨ proper noun ⟩ that can later on exist used by writing ( ⟨ name ⟩ cs: ⟨ arguments ⟩ ). When TikZ encounters a coordinate specified in this mode, the ⟨ arguments ⟩ are passed to ⟨ code ⟩ every bit argument #ane.
It is now the job of ⟨ lawmaking ⟩ to make sense of the ⟨ arguments ⟩. At the end of ⟨ code ⟩, the two TeX dimensions \pgf@x and \pgf@y should exist accept the \(ten\)- and \(y\)-sheet coordinate of the coordinate.
Information technology is not necessary, but customary, to parse ⟨ arguments ⟩ using the key–value syntax. Even so, y'all tin can as well parse it in whatsoever way y'all similar.
In the following example, a coordinate organisation cylindrical is defined.
\tikzaliascoordinatesystem {⟨ new name ⟩}{⟨ old name ⟩} ¶
Creates an allonym of ⟨ old name ⟩.
xiii.3Coordinates at Intersections¶
Y'all will wish to compute the intersection of two paths. For the special and frequent case of two perpendicular lines, a special coordinate arrangement chosen perpendicular is available. For more general cases, the intersection library tin be used.
thirteen.3.oneIntersections of Perpendicular Lines¶
A frequent special case of path intersections is the intersection of a vertical line going through a point \(p\) and a horizontal line going through some other point \(q\). For this situation in that location is a useful coordinate arrangement.
Coordinate system perpendicular ¶
Yous can specify the two lines using the following keys:
/tikz/cs/horizontal line through ={( ⟨ coordinate ⟩ )} (no default) ¶
Specifies that one line is a horizontal line that goes through the given coordinate.
/tikz/cs/vertical line through ={( ⟨ coordinate ⟩ )} (no default) ¶
Specifies that the other line is vertical and goes through the given coordinate.
However, in nigh all cases you should, instead, employ the implicit syntax. Hither, you write ( ⟨ p ⟩ |- ⟨ q ⟩ ) or ( ⟨ q ⟩ -| ⟨ p ⟩ ).
For example, (2,1 |- 3,4) and (3,4 -| 2,1) both yield the same as (two,four) (provided the \(xy\)-coordinate system has not been modified).
The well-nigh useful application of the syntax is to draw a line up to some point on a vertical or horizontal line. Here is an instance:
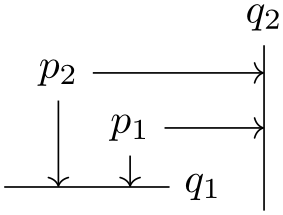
Notation that in ( ⟨ c ⟩ |- ⟨ d ⟩ ) the coordinates ⟨ c ⟩ and ⟨ d ⟩ are not surrounded by parentheses. If they need to exist complicated expressions (similar a computation using the $-syntax), you lot must environment them with braces; parentheses will then be added around them.
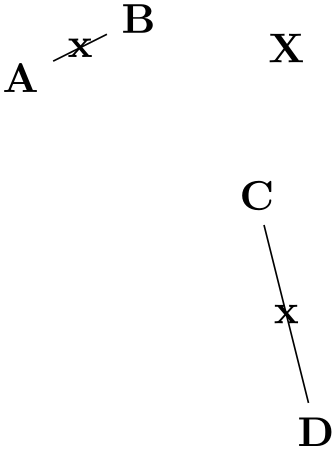
As an example, let usa specify a point that lies horizontally at the middle of the line from \(A\) to \(B\) and vertically at the middle of the line from \(C\) to \(D\):
13.3.2Intersections of Arbitrary Paths¶
TigZ Library intersections ¶
\usetikzlibrary{intersections} % LaTeX and plain TeX
\usetikzlibrary[intersections] % Con TeX t
This library enables the adding of intersections of ii arbitrary paths. Even so, due to the low accuracy of TeastTen , the paths should not be "too complicated". In detail, you should non try to intersect paths consisting of lots of very modest segments such as plots or decorated paths.
To observe the intersections of two paths in Tione thousandZ, they must be "named". A "named path" is, quite but, a path that has been named using the following key (annotation that this is a different cardinal from the name key, which but attaches a hyperlink target to a path, but does not store the path in a way the is useful for the intersection ciphering):
/tikz/name path = ⟨ name ⟩ (no default) ¶
/tikz/proper name path global = ⟨ proper noun ⟩ (no default) ¶
The effect of this cardinal is that, after the path has been constructed, but earlier information technology is used, it is associated with ⟨ proper name ⟩. For name path, this association survives across the terminal semi-colon of the path simply non the end of the surrounding scope. For name path global, the association will survive beyond whatever scope as well. Handle with care.
Any paths created by nodes on the (main) path are ignored, unless this key is explicitly used. If the same ⟨ proper noun ⟩ is used for the main path and the node path(southward), then the paths will exist added together so associated with ⟨ name ⟩.
To observe the intersection of named paths, the following cardinal is used:
/tikz/name intersections ={⟨ options ⟩} (no default) ¶
This key changes the primal path to /tikz/intersection and processes ⟨ options ⟩. These options decide, amongst other things, which paths to utilize for the intersection. Having processed the options, whatever intersections are then found. A coordinate is created at each intersection, which past default, will be named intersection-1, intersection-2, then on. Optionally, the prefix intersection tin can be changed, and the total number of intersections stored in a TeastX -macro.
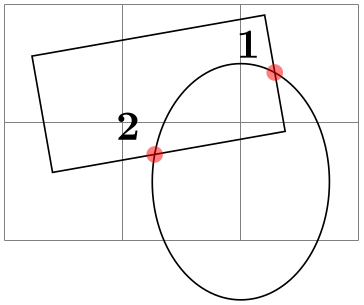
The following keys can exist used in ⟨ options ⟩:
/tikz/intersection/of = ⟨ name path 1 ⟩ and ⟨ name path 2 ⟩ (no default) ¶
This key is used to specify the names of the paths to apply for the intersection.
/tikz/intersection/name = ⟨ prefix ⟩ (no default, initially intersection) ¶
This key specifies the prefix proper noun for the coordinate nodes placed at each intersection.
/tikz/intersection/total = ⟨ macro ⟩ (no default) ¶
This fundamental means that the total number of intersections constitute volition be stored in ⟨ macro ⟩.
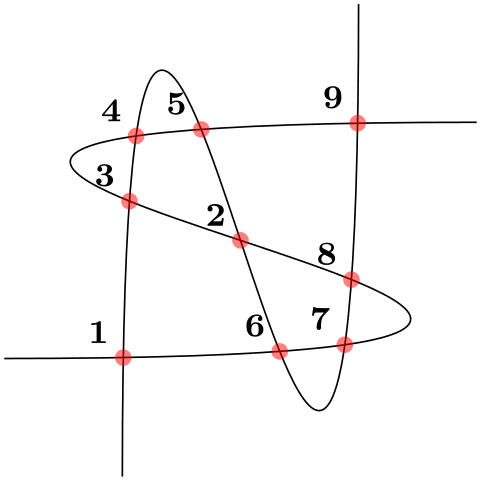
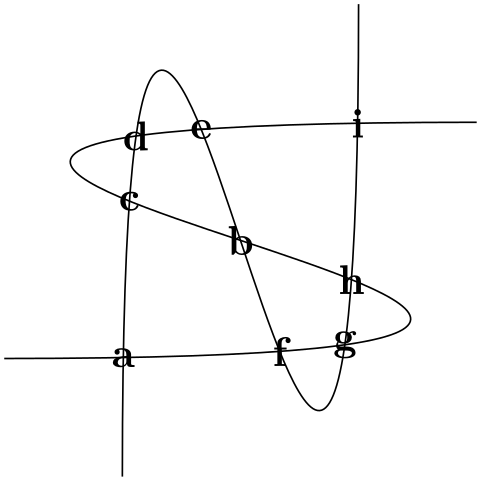
\fill [name intersections={of=bend 1 and curve ii, name=i, total=\t}] \usetikzlibrary {intersections}
\begin{tikzpicture}
\clip(-2,-2)rectangle (2,two);
\describe [name path=curve 1](-2,-ane) ..controls (8,-1)and (-8,ane) ..(2,one);
\draw [name path=bend ii](-1,-2) ..controls (-1,8)and (i,-8) ..(1,2);
[red,opacity=0.5,every node/.mode={above left,black,opacity=i}]
\foreach\southwardin {ane,...,\t}{(i-\s)circle (2pt)node {\footnotesize \south}};
\finish{tikzpicture}
/tikz/intersection/by = ⟨ comma-separated list ⟩ (no default) ¶
This primal allows you to specify a list of names for the intersection coordinates. The intersection coordinates will however be named ⟨ prefix ⟩ - ⟨ number ⟩, only additionally the first coordinate will also be named past the beginning element of the ⟨ comma-separated list ⟩. What happens is that the ⟨ comma-separated list ⟩ is passed to the \foreach statement and for ⟨ list member ⟩ a coordinate is created at the already-named intersection.
\fill [name intersections={of=curve 1 and curve 2, by={a,b}}] \usetikzlibrary {intersections}
\begin{tikzpicture}
\clip(-2,-2)rectangle (2,2);
\draw [proper name path=bend 1](-two,-1) ..controls (eight,-i)and (-8,1) ..(2,1);
\describe [proper noun path=curve 2](-one,-2) ..controls (-i,eight)and (1,-8) ..(i,2);
(a)circumvolve (2pt)
(b)circumvolve (2pt);
\finish{tikzpicture}
You tin also utilise the ... note of the \foreach statement inside the ⟨ comma-separated list ⟩.
In case an chemical element of the ⟨ comma-separated list ⟩ starts with options in square brackets, these options are used when the coordinate is created. A coordinate proper noun can all the same, merely need not, follow the options. This makes it easy to add together labels to intersections:
\fill [name intersections={ \usetikzlibrary {intersections}
\begin{tikzpicture}
\prune(-2,-ii)rectangle (2,2);
\draw [name path=bend one](-2,-1) ..controls (viii,-1)and (-8,1) ..(2,1);
\describe [name path=curve 2](-1,-two) ..controls (-one,8)and (1,-viii) ..(one,2);
of=curve 1 and curve 2,
by={[characterization=center:a],[label=centre:...],[characterization=center:i]}}];
\end{tikzpicture}
/tikz/intersection/sort past = ⟨ path proper noun ⟩ (no default) ¶
By default, the intersections are only returned in the lodge that the intersection algorithm finds them. Unfortunately, this is not necessarily a "helpful" ordering. This primal can be used to sort the intersections along the path specified by ⟨ path name ⟩, which should be one of the paths mentioned in the /tikz/intersection/of cardinal.
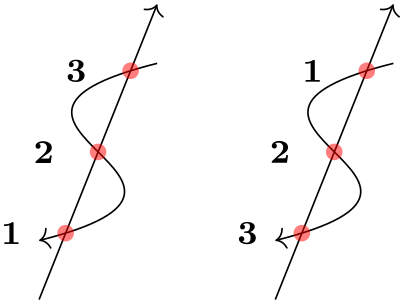
\usetikzlibrary {intersections}
\brainstorm{tikzpicture}
\prune(-0.5,-0.75)rectangle (three.25,2.25);
\foreach\pathname/ \shiftin {line/0cm,curve/2cm}{
\tikzset{xshift= \shift }
\describe [->,name path=curve](1,1.5) ..controls (-one,1)and (2,0.5) ..(0,0);
\draw [->,proper name path=line](0,-.v)-- (1,2) ;
\fill [proper noun intersections={of=line and curve,sort by=\pathname, proper noun=i}]
[red,opacity=0.5,every node/.style={left=.25cm,blackness,opacity=1}]
\foreach\sin {i,2,3}{(i-\southward)circle (2pt)node {\footnotesize \s}};
}
\finish{tikzpicture}
13.4Relative and Incremental Coordinates¶
13.iv.1Specifying Relative Coordinates¶
You tin can prefix coordinates by ++ to make them "relative". A coordinate such every bit ++(1cm,0pt) means "1cm to the right of the previous position, making this the new current position". Relative coordinates are often useful in "local" contexts:
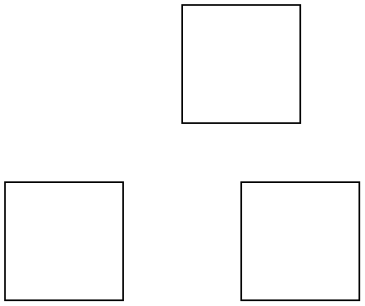
\begin{tikzpicture}
\describe(0,0)-- ++ (i,0)-- ++ (0,one)-- ++ (-1,0)-- bicycle;
\describe(2,0)-- ++ (i,0)-- ++ (0,1)-- ++ (-ane,0)-- bike;
\draw(1.5,ane.5)-- ++ (1,0)-- ++ (0,1)-- ++ (-one,0)-- cycle;
\finish{tikzpicture}
Instead of ++ you tin can likewise utilize a single +. This too specifies a relative coordinate, but it does not "update" the electric current point for subsequent usages of relative coordinates. Thus, you can use this notation to specify numerous points, all relative to the same "initial" bespeak:
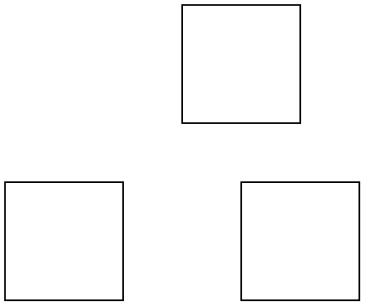
\begin{tikzpicture}
\draw(0,0)-- + (i,0)-- + (1,ane)-- + (0,1)-- cycle;
\describe(2,0)-- + (1,0)-- + (ane,1)-- + (0,1)-- cycle;
\draw(1.5,1.5)-- + (1,0)-- + (i,1)-- + (0,1)-- cycle;
\finish{tikzpicture}
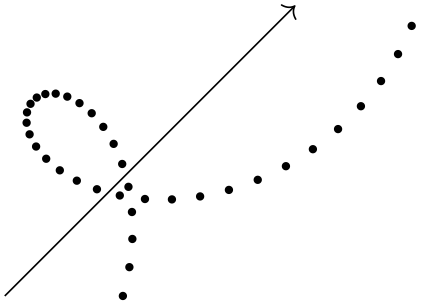
There is a special situation, where relative coordinates are interpreted differently. If y'all use a relative coordinate as a control indicate of a Bézier curve, the post-obit rule applies: First, a relative first command betoken is taken relative to the start of the curve. Second, a relative second control point is taken relative to the end of the curve. 3rd, a relative finish point of a curve is taken relative to the start of the bend.
This special behavior makes information technology piece of cake to specify that a curve should "leave or make it from a certain management" at the start or cease. In the following example, the bend "leaves" at \(xxx^\circ \) and "arrives" at \(60^\circ \):
13.4.2Rotational Relative Coordinates¶
You lot may sometimes wish to specify points relative not only to the previous point, merely additionally relative to the tangent entering the previous point. For this, the following central is useful:
/tikz/plough (no value) ¶
This key tin be given as an option to a ⟨ coordinate ⟩ as in the following instance:

\tikz\describe(0,0)-- (ane,1)-- ([turn]-45:1cm)-- ([plow]-30:1cm);
The effect of this fundamental is to locally shift the coordinate arrangement so that the terminal indicate reached is at the origin and the coordinate organization is "turned" and then that the \(x\)-axis points in the direction of a tangent entering the last point. This ways, in effect, that when you apply polar coordinates of the form ⟨ relative angle ⟩ : ⟨ distance ⟩ together with the turn option, you specify a betoken that lies at ⟨ altitude ⟩ from the last point in the direction of the last tangent entering the concluding point, but with a rotation of ⟨ relative angle ⟩.
This key as well works with curves …

…and with plots …

\tikz\drawplot coordinates {(0,0)(ane,1)(2,0)(iii,0) }-- ([turn]thirty:1cm);
Although the higher up examples utilise polar coordinates with plow, you can likewise use whatever normal coordinate. For example, ([plough]1,1) will suspend a line of length \(\sqrt 2\) that is turns by \(45^\circ \) relative to the tangent to the terminal point.

\tikz\draw(0.five,0.5)-| (ii,1)-- ([turn]1,1)
..controls ([plow]0:1cm) ..([turn]-90:1cm);
thirteen.4.3Relative Coordinates and Scopes¶
An interesting question is, how practice relative coordinates behave in the presence of scopes? That is, suppose we use curly braces in a path to make part of it "local", how does that affect the electric current position? On the ane hand, the current position certainly changes since the telescopic only affects options, not the path itself. On the other paw, it may be useful to "temporarily escape" from the updating of the current point.
Since both interpretations of how the current point and scopes should "interact" are useful, in that location is a (local!) option that allows you to decide which you need.
/tikz/electric current point is local = ⟨ boolean ⟩ (no default, initially simulated) ¶
Normally, the scope path operation has no effect on the current point. That is, curly braces on a path have no effect on the current position:

If you set this cardinal to truthful, this behavior changes. In this case, at the end of a grouping created on a path, the concluding electric current position reverts to whatever value information technology had at the start of the scope. More precisely, when TikZ encounters } on a path, it checks whether at this particular moment the fundamental is set to truthful. If then, the current position reverts to the value it had when the matching { was read.

In the above instance, we could also have given the choice outside the scope, for example as a parameter to the whole scope.
thirteen.5Coordinate Calculations¶
TikZ Library calc ¶
\usetikzlibrary{calc} % FiftyaTdue eastX and plain TeastTen
\usetikzlibrary[calc] % Con Teast10 t
You lot need to load this library in order to use the coordinate calculation functions described in the present section.
It is possible to do some bones calculations that involve coordinates. In essence, you lot can add together and decrease coordinates, scale them, compute midpoints, and do projections. For instance, ($(a) + ane/3*(1cm,0)$) is the coordinate that is \(1/iii \text {cm}\) to the right of the point a:
thirteen.5.oneThe Full general Syntax¶
The general syntax is the post-obit:
( [ ⟨ options ⟩ ] \(|\meta {coordinate computation}|\)) .
Every bit yous can see, the syntax uses the TeX math symbol $ to betoken that a "mathematical ciphering" is involved. However, the $ has no other effect, in particular, no mathematical text is typeset.
The ⟨ coordinate ciphering ⟩ has the following structure:
-
1. Information technology starts with
⟨ cistron ⟩ * ⟨ coordinate ⟩ ⟨ modifiers ⟩
-
2. This is optionally followed by + or - then another
⟨ gene ⟩ * ⟨ coordinate ⟩ ⟨ modifiers ⟩
-
3. This is once more followed by + or - and another of the above modified coordinate; and then on.
In the following, the syntax of factors and of the different modifiers is explained in item.
thirteen.5.iiThe Syntax of Factors¶
The ⟨ factor ⟩s are optional and detected past checking whether the ⟨ coordinate computation ⟩ starts with a (. Also, after each \(\pm \) a ⟨ factor ⟩ is present if, and only if, the + or - sign is non directly followed by(.
If a ⟨ factor ⟩ is present, information technology is evaluated using the \pgfmathparse macro. This means that you lot can employ pretty complicated computations inside a gene. A ⟨ factor ⟩ may even incorporate opening parentheses, which creates a complication: How does TikZ know where a ⟨ factor ⟩ ends and where a coordinate starts? For instance, if the offset of a ⟨ coordinate computation ⟩ is 2*(three+4…, it is not clear whether 3+4 is role of a ⟨ coordinate ⟩ or role of a ⟨ factor ⟩. Because of this, the post-obit rule is used: Once it has been determined, that a ⟨ factor ⟩ is nowadays, in principle, the ⟨ factor ⟩ contains everything upwardly to the next occurrence of *(. Note that there is no space betwixt the asterisk and the parenthesis.
Information technology is permissible to put the ⟨ factor ⟩ in curly braces. This tin can be used whenever it is unclear where the ⟨ factor ⟩ would end.
Here are some examples of coordinate specifications that consist of exactly one ⟨ gene ⟩ and one ⟨ coordinate ⟩:
thirteen.5.3The Syntax of Partway Modifiers¶
A ⟨ coordinate ⟩ tin be followed by different ⟨ modifiers ⟩. The outset kind of modifier is the partway modifier. The syntax (which is loosely inspired by Uwe Kern's xcolor package) is the post-obit:
⟨ coordinate ⟩ ! ⟨ number ⟩ ! ⟨ angle ⟩ : ⟨ 2d coordinate ⟩
One could write for case
(1,2) !.75! (3,four)
The pregnant of this is: "Employ the coordinate that is three quarters on the way from (1,2) to (3,iv)." In general, ⟨ coordinate x ⟩ ! ⟨ number ⟩ ! ⟨ coordinate y ⟩ yields the coordinate \((one - \meta {number})\meta {coordinate ten} + \meta {number} \meta {coordinate y}\). Note that this is a bit unlike from the manner the ⟨ number ⟩ is interpreted in the xcolor packet: First, you use a cistron between \(0\) and \(1\), not a percentage, and, 2nd, as the ⟨ number ⟩ approaches \(i\), we approach the 2d coordinate, non the first. Information technology is permissible to utilise a ⟨ number ⟩ that is smaller than \(0\) or larger than \(one\). The ⟨ number ⟩ is evaluated using the \pgfmathparse command and, thus, it can involve complicated computations.
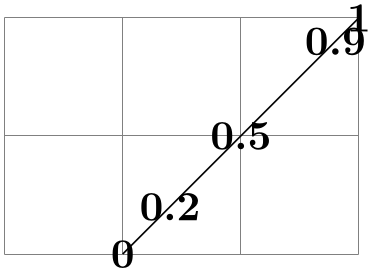
\depict(1,0)-- (3,ii); \foreach\iin {0,0.2,0.5,0.9,1} \usetikzlibrary {calc}
\begin{tikzpicture}
\describe [assistance lines](0,0)grid (3,2);
\nodeat ($(1,0) ! \i ! (iii,2) $) {\i};
\finish{tikzpicture}
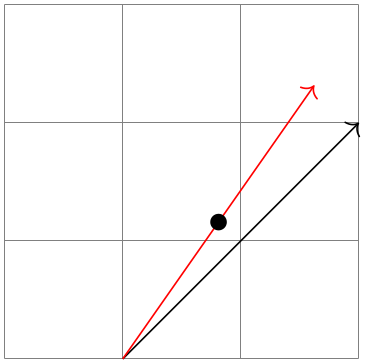
The ⟨ second coordinate ⟩ may be prefixed by an ⟨ angle ⟩, separated with a colon, as in (one,1)!.v!60:(2,2). The general significant of ⟨ a ⟩ ! ⟨ factor ⟩ ! ⟨ angle ⟩ : ⟨ b ⟩ is: "First, consider the line from ⟨ a ⟩ to ⟨ b ⟩. Then rotate this line by ⟨ angle ⟩ effectually the signal ⟨ a ⟩ . Then the two endpoints of this line volition be ⟨ a ⟩ and some point ⟨ c ⟩. Use this point ⟨ c ⟩ for the subsequent computation, namely the partway ciphering."
Here are two examples:
You lot can repeatedly apply modifiers. That is, after whatever modifier y'all can add together another (possibly different) modifier.
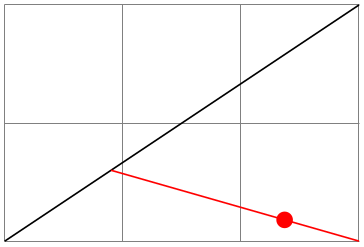
\draw(0,0)-- (3,2); \usetikzlibrary {calc}
\brainstorm{tikzpicture}
\depict [help lines](0,0)grid (iii,2);
\draw[red]($(0,0) !.3! (iii,2) $)-- (three,0);
\fill[ruddy]($(0,0) !.3! (3,2) !.7! (3,0) $)circle (2pt);
\stop{tikzpicture}
13.5.4The Syntax of Distance Modifiers¶
A altitude modifier has almost the same syntax equally a partway modifier, only you use a ⟨ dimension ⟩ (something like 1cm) instead of a ⟨ factor ⟩ (something like 0.v):
⟨ coordinate ⟩ ! ⟨ dimension ⟩ ! ⟨ angle ⟩ : ⟨ second coordinate ⟩
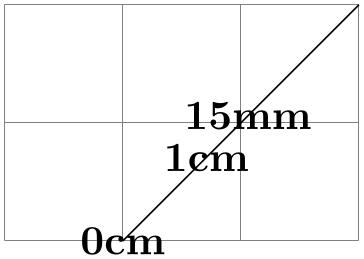
When you write ⟨ a ⟩ ! ⟨ dimension ⟩ ! ⟨ b ⟩, this ways the following: Utilise the point that is distanced ⟨ dimension ⟩ from ⟨ a ⟩ on the straight line from ⟨ a ⟩ to ⟨ b ⟩. Here is an instance:
Equally before, if you use a ⟨ angle ⟩, the ⟨ second coordinate ⟩ is rotated by this much around the ⟨ coordinate ⟩ earlier it is used.
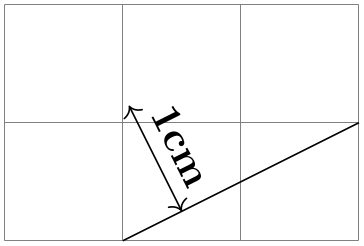
The combination of an ⟨ angle ⟩ of 90 degrees with a distance tin can be used to "offset" a signal relative to a line. Suppose, for instance, that y'all have computed a point (c) that lies somewhere on a line from (a) to(b) and y'all now wish to offset this point by 1cm so that the distance from this offset point to the line is 1cm. This can be accomplished equally follows:
thirteen.5.5The Syntax of Projection Modifiers¶
The projection modifier is also similar to the to a higher place modifiers: Information technology as well gives a signal on a line from the ⟨ coordinate ⟩ to the ⟨ second coordinate ⟩. However, the ⟨ number ⟩ or ⟨ dimension ⟩ is replaced by a ⟨ projection coordinate ⟩:
⟨ coordinate ⟩ ! ⟨ project coordinate ⟩ ! ⟨ angle ⟩ : ⟨ 2d coordinate ⟩
Here is an case:
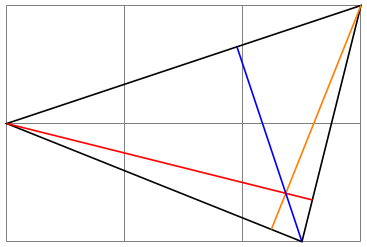
(ane,2) ! (0,5) ! (3,4)
The effect is the following: Nosotros project the ⟨ projection coordinate ⟩ orthogonally onto the line from ⟨ coordinate ⟩ to ⟨ second coordinate ⟩. This makes information technology like shooting fish in a barrel to compute projected points:
alfordandesch1958.blogspot.com
Source: https://tikz.dev/tikz-coordinates
0 Response to "Draw Circle Between Points Tikz"
Publicar un comentario